Интересное за неделю

IT тематика

• Подоборка интересных плюшек по PostgresSQL.
• Про AWS доступным языком - сводная таблица названий сервисов от Amazon с описанием.
• Введение в Machine Learning с красивой графикой.
• Увесистая подборка книг(более 60-и) в свободном доступе по Data Science, Data Mining и Machine Learning.
• Микросервисы без серверов.
• О том как работают реляционные БД.
• Прикольный видос поясняющий, как работала видеоподсистема в старых игровых консолях(в условиях ограниченных системных ресурсов).
• Подборка советов по Haskell для изучаюших этот язык.

Github

• Колода карт на HTML5.
• Git Radar - приглашение командной строки с отображением доп. информации о препозитарии.

Оффтоп

• Британскай библиотека выложила около 1М картинок в открытый доступ.
• Игра под названием LSD. Не то что подумал :). Расшифровывается как Line Square Dot.
• Онлайн редактор с поддеркой Md и LaTex.
• Hack - шрифт для редакторов кода.

Интересное за неделю

IT тематика

• Postgres CLI - клиент для Postgres выполненый в виде интерпритатора с автодополнением ключевых слов, таблиц и т.д. Тоже самое для MySQL, только, похоже, на данный момент еще в нерабочем состоянии.
• Spark - легковестный вэб фреймворк. Нелязя назвать альтернативой спринг MVC, но для быстрого прототипирования - самое оно.
• Ceramic - утилита конвертации вэб приложения в нативное. Из особенностей... Написана на Lisp-е. Из приятного - есть порты под разные платформы.
• Для пользвателей Mac OS - полезные плюшки для iTerm2.
• Построение API Gateway при помощи Amazon. Если коротко: The API Gateway makes it easy for you to connect all types of applications to API implementations that run on AWS Lambda, Amazon Elastic Compute Cloud (EC2), or a publicly addressable service hosted outside of AWS. If you use Lambda (I’ll show you how in just a moment), you can implement highly scalable APIs that are totally server-less.
• Из мира Android разработки о том как красиво грузить данные из различных источников.
• Казел ли твой пользователь. Небольшой обзор забавных(и тем не мение реальных) названий методов и правил в Android SDK.

Оффтоп

• Для любителей рисунка - история становления художника от самого начала(с примерами работ), до текущего момента с описание где и как учился.
• Для любителей шахмат. Понравился раздел по прокачиванию своих скилов в тактике. Увесистая подборка задач. Хотя должен признаться, что есть весьма примитивные, но в общем и целом - неплохо.

Запись рабочей сессии терминала

Коротенький пост о том как записать рабочую сессию своего терминала. Можно как по старинке - сделать видеозахват, но приимущество этого способа в том, что есть возможность копипаститы прям из видео. Для примера:

Задача "Скобки"

Не так давно нарвался на интересную задачку в блоге своего знакомого. Дано:

Given a string containing just the characters '(' and ')', find the length of the longest valid (well-formed) parentheses substring. For "(()", the longest valid parentheses substring is "()", which has length = 2. Another example is ")()())", where the longest valid parentheses substring is "()()", which has length = 4.

Или по русски: необходимо найти максимальнодлинную валидную последовательность состаящую из парных скобок. Выражение может быть как вложенным "(())"(с неограниченной глубиной) так и последовательным "()()" с неограниченной длинной, так и состоять из комбинации первых двух. При чем как видно из условия, в выражении могут присутствовать непарные скобки. Так же на просторах можно найти упрощенный вариант - лишь определить валидность выражения, но наша(задача) несколько интересней.

Статья на которую я ссылаюсь дает простое и хорошее решение, но мне захотелось усложнить условия - не использовать стэк. Юнит тест:

@Test
public void testFind() {
    assertEquals(Reference.find("("), Solution.find("("));
    assertEquals(Reference.find(")"), Solution.find(")"));
    assertEquals(Reference.find(")("), Solution.find(")("));
    assertEquals(Reference.find("()"), Solution.find("()"));
    assertEquals(Reference.find("()()"), Solution.find("()()"));
    assertEquals(Reference.find("(()"), Solution.find("(()"));
    assertEquals(Reference.find("(())"), Solution.find("(())"));
    assertEquals(Reference.find("())(()()"), Solution.find("())(()()"));
    assertEquals(Reference.find("(((()())))"), Solution.find("(((()())))"));
    assertEquals(Reference.find("(((((()()))))"), Solution.find("(((((()()))))"));
    assertEquals(Reference.find("()(())"), Solution.find("()(())"));
    assertEquals(Reference.find(")()())"), Solution.find(")()())"));
    assertEquals(Reference.find("()(()"), Solution.find("()(()"));
}

Где:

• Reference.find(String string) - эталонная реализация
• Solution.find(String string) - решение

Первое

Поигравшись с неправильными решениями(а их было около трех), пришел к следующей модели. Легко заметить, что выражение можно представить в виде перевернутого дерева, где узел - это одна валидная группа состоящая из открывающей и закрывающей скобки плюс вложенные(дочерне ноды). Минимальновалидная нода - это выражение вида "()".

Рессмотрим строку:

(())(()

Тогда первая валидная группа будет иметь следующий вид:

А все выражение целиком состоять из трех подгурпп:

• "(())" - валидная(закрытая или парная) группа длинной 4
• "(" - невалидня группа длинной 1
• "()" - валидная группа длинной 2

Конечное решение выглядит так - обходим строку, пытаясь найти валидную группу начиная с нулевого элемента. Есть два возможных случая:

• Группа парная - производим смещение на позицию вправо равную длинне группы. Если группы идут одна за одной без разрыва, то накапливаем дилнну в нек. переменную-счетчик, если происходит разрыв, то сравниваем накопленное значение с максимальным
• Группа непарная - пропускаем данный элемент и повторяем операцию поиска группы

public class Solution {

    static final class Node {
        int offset;
        int len;
        List<Node> nodes;

        Node(int offset, int len, List<Node> nodes) {
            this.offset = offset;
            this.len = len;
            this.nodes = nodes;
        }

        Node(int offset, int len) {
            this(offset, len, null);
        }

        @Override
        public String toString() {
            return "[offset=" + offset + ", len=" + len + ", child=" + nodes + "]";
        }
    }

    static int find(String string) {
        int max = 0;
        int accumulator = 0;

        for (int i = 0; i < string.length(); i++) {
            Node node = getNode(string, i);
            if (node == null) {
                max = Math.max(max, accumulator);
                accumulator = 0;
                continue;
            }

            accumulator += node.len;
            i += (node.len - 1);
        }

        return Math.max(max, accumulator);
    }


    static Node getNode(final String string, final int offset) {
        if (offset >= string.length()) return null;

        List<Node> nodes = new ArrayList<Node>(0);
        int nodesLen = 0;

        if (string.charAt(offset) == '(') {
            int rightIndex = offset + 1;
            if (rightIndex >= string.length()) return null;

            boolean right = string.charAt(rightIndex) == ')';
            if (right) return new Node(offset, 2);

            for (int i = (offset + 1); i < string.length(); i++) {
                Node node = getNode(string, i);

                if (node != null) {
                    nodes.add(node);
                    i += (node.len - 1);
                    nodesLen += node.len;
                }
            }
            if (nodes.isEmpty()) return null;

            rightIndex = offset + nodesLen + 1;
            if (rightIndex >= string.length()) return null;

            right = string.charAt(rightIndex) == ')';
            if (right) return new Node(offset, 2 + nodesLen, nodes);
        }

        return null;
    }
}

Как можно заметить есть ряд существенных недостатков, а именно:

• Рекурсия - при большой глубине вложенности скобок, запустив тест, гарантированно получим переполнение стэка
• Громоздкость - что не говори, а строить дерево относительно ресурсоемкая операция по сравнению с оригинальным решением
• Время работы(пересекается с предыдущим) - далеко не самое лучшее

Чуть позже я немного упростил код - убрал класс Node, оставив лишь только длинну группы(метод getNode - возвращет не экземпляр класса, а значение типа integer). Но приводить код смысла нет, т.к. в основе лежит все та же убогая идея.

Второе

Позже сфорировал ряд дополнительных требований к реализации - она должно быть итеративной и не такой ресуроемкой. За основу взял следующую идею - объявляем переменные:

• left - счетчик окрывающих скобок. Делаем инкремент каждый раз когда всречается окрывающая скобка.
• right - счетчик закрывающих скобок. Делаем инкремент каждый раз когда всречается закрывающая скобка.
• pair - счетчик валидных пар. Делаем инкремент каждый раз когда счетчик left и right больше нуля.

Последоватлеьно обхоим всю строку, так же как и в предыдущем варианте пытаемся найти валидную(закрытую) группу, но делаем это не рекурсивно, а итеративно. Встречая валидную группу, смещаемся в право по строке на ее длинну. В случае невалидной группы - смещаемя вправо на один символ. Строка разбитая на группы будет выглядеть следующим образом:

А решение целиком:

public class Solution {


    static int find(String string) {
        int max = 0, len = 0;
        for (int i = 0; i < string.length(); i++) {
            int n = find(string, i);
            if (n > 0) {
                len += n;
                i += (n - 1);
            } else {
                max = Math.max(len, max);
                len = 0;
            }
        }
        return Math.max(len, max);
    }

    static int find(String string, int index) {
        int left = 0, right = 0, pair = 0;
        for (int i = index; i < string.length(); i++) {

            if (string.charAt(i) == '(') {
                left++;
            } else {
                if (left <= 0) continue;
                right++;
            }

            if (left > 0 && right > 0) {
                left--;
                right--;
                pair++;
            }

            if (left == 0 && right == 0) break;
        }
        return (left == 0 && right == 0) ? pair * 2 : 0;
    }
}

Ресурсы

• Оригинальная статья
• Упрощенная вариация задачи
• Проект на bitbucket-е(по хронологии): раз, два, три

Немного о генераторе случайных чисел

Все кто программирует на java должен был слыхать хотя бы раз о Random. В javadoc о нем пишут следующее:

Класс служит для генерации потока псевдослучайных чисел, использует 48-битный seed, который изменяется по средством литейной конгруэнтной формулы. И ссылка к Дональду Кнуту на The Art of Computer Programming, Volume 2, Section 3.2.1.

В общем, цель данного поста проверить на сколько приемлемый результат обеспечивает стандартный генератор. Плюс на просторах я нашел улучшенную версию, заодно проверю и его.

Тест выглядит следующим образом. Создадим массив из ста элементов. По индексу храним счетчик значений. Запускать будем в однотонном режиме, дабы как говорит документация у нас не просела производительность. Пару слов о том, что я ожидаю получить в качестве результата. В идеальном случае значения счетчиков в массиве по окончанию работы должны стремиться к некой величине, а именно N/100, где N - это общее количество сгенерированных значений. Понятно, что на практике у нас будут отклонения, а вот какого порядка - это собственно и хочется узнать.

Тестировать будем сразу три ГСЧ:

• Стандартный Random
• Улучшенный Random
• ThreadLocalRandom

Поначалу хотел, чтоб каждый ГСЧ отработа Long.MAX_VALUE циклов, это бы обеспечило более достоверные результаты, но по времени это получалось уже как-то затратно.

public class Main {
    static final Random STANDARD_RANDOM = new Random();
    static final Random IMPROVED_RANDOM = new HighQualityRandom();

    static final int[] STANDARD_RANDOM_RESULT = new int[100];
    static final int[] IMPROVED_RANDOM_RESULT = new int[100];
    static final int[] THREAD_LOCAL_RANDOM_RESULT = new int[100];

    public static void main(String[] args) {
        for (long i = 0; i < 1000000000l; i++) {
            STANDARD_RANDOM_RESULT[STANDARD_RANDOM.nextInt(100)]++;
            IMPROVED_RANDOM_RESULT[IMPROVED_RANDOM.nextInt(100)]++;
            THREAD_LOCAL_RANDOM_RESULT[ThreadLocalRandom.current().nextInt(100)]++;
        }

        for (int i = 0; i < STANDARD_RANDOM_RESULT.length; i++) {
            System.out.println(i
                            + " " + STANDARD_RANDOM_RESULT[i]
                            + " " + IMPROVED_RANDOM_RESULT[i]
                            + " " + THREAD_LOCAL_RANDOM_RESULT[i]
            );
        }
    }
}

Скажу сразу, я ожидал худшего. Поясню, что значит худшее в данном контексте. Если провести регрессию, например линейную, то плохим результатом можно было бы считать, когда прямая идет под каким либо углом по отношению к оси X. Это значит, что ГСЧ имеет склонность выдвать значения неравномерно. В нашем же случае, выглядит так, что подобных завалов нет и при бОльшем количестве сгенерируемых чисел, кривая бы походила на прямую которая параллельна оси Х.

Пару слов о ThreadLocalRandom/ Добавлять его смысла особого не было. Исходники я не смотрел, но подозреваю, что целиком и полность это тот жесамый Random, только обернутый в ThreadLocal класс. Если ГСЧ используется в многопоточной среде, то рекомендуется испльзовать именно его в противовес обычному Random-у. Даже не смотря на то, что второй объявлен как thread safe.

Выводы

По наивности своей думал, что псевдослучайный означает непригодный для практического применения. Что в корне неверно. В интернетах пишут же, что для подобных типов генераторов можно найти закономерности(алгоритм гарантирующий угадывание следующего числа). Есть сомнения на этот счет. Для некоторых типов приложений(напрмер игры) стандартный ГСЧ может быть вполне приемлемым.

Ресурсы

• Стандартный генератор Random
• Улучшенная версия генератора
• Про линейный конгруэнтный метод
• Класс о существовании которого я не знал к своему стыду ThreadLocalRandom
• Gnuplot вэб версия

Как работают Слот Машины

Заинтересовался данной темой и как оно бывает, материалов не столь много как хотелось бы.  Планируется 2-е части. 1-я - теория,  2-я(если дойдут руки) - практика или реализация. Основная часть информации взята из этой статьи статьи.

Случайность

Работа слот машина как и любой другой игры в казино базируется на следующих принципах:

• Результат каждого раунда случайный(выпавшая комбинация костей, раздача карт, вращения колеса барабана)
• Выигрыш всегда меньше фактического(об этом чуть ниже)

Другими словами, казино имеет преимущество подкрепленное математической моделью, как следствие, нет необходимости жульничать. Выпадающие символы случайны, но все устроено так, что  в долгосрочной перспективе вы проигрываете. Тем не мение, люди пытаются отыскать выигрышные шаблоны или выигрышные алгоритмы. Внутреннее чувство иногда подсказывает им, что машины работают на горячих или холодных циклах, что они отдают больше(или меньше) в разное время дня - все это не так.

Абсолютно не важно, сколько времени прошло с момента последнего джек-пота. Шансы на выигрыш каждого спина от этого не меняются. Нет никакого “потому что…” из-за чего выпала выигрышная комбинация. Не может быть алгоритма или шаблона обеспечивающего победу игрока.

Простейшая слот машина

Для начала простой пример. Рассмотрим игру подбрасывание монеты(он же coin-flip):

• вы делаете ставку в 1$
• подбрасываем монету
• выпадет орел - вы выигрываете 1$. Решка - выигрывает казино

Легко заметить, что играя продолжительное время каждый останется при своих(even-sum game). Т.е. количество выпадений с орлом будет стремиться к 50%. Это значит, что казино остается без прибыли(ровно как и вы), поэтому подобные модели не используются. Теперь внесем поправку:

• если выпадает решка, казино выигрывает как и обычно 1$
• если орел, то вы выигрываете не 1$, а 0.9$ 

Не нужно быть великим математиком, чтоб догадаться, играя при таких правилах играя всегда останешься в убытке:

• в среднем на каждый поставленный доллар игрок получает 95 центов в случае выигрыша
• соответственно казино получает 5 центов в качестве прибыли

Особо внимательные могут заметить, среднее значение потерь должно быть 10, а не 5 центов, но тут следует помнить, что казино забирает эти деньги лишь в случае выигрыша, что приблизительный составляет 50% от общего числа брошенных монет.

Теперь предположим, что казино хочет обратить наш coin-flip в машину. Алгоритм был бы предельно простым: генерируем случайное значение 1 или 0 и платим победителю 90% в случае выигрыша.

Все что вам нужно было узнать из этого примера - казино должно обеспечить случайное выпадение значений. Чем дольше вы играете, тем больше проигрываете в перспективе.

Комбинации

Вернемся к слотам. Значение отдельного колеса формируется произвольным образом генератором случайный чисел(он же ГСЧ) в рамках заданного диапазона. Каждому значению колеса соответсвует стоп-символ, который и будет отображен на экране или барабане в момент его остановки.

Когда колеса еще крутятся, игра уже закончена. ГСЧ сгенерировал финальную комбинацию. По правде говоря, слот машинам даже не нужны барабаны и экран, можно обойтись лишь простейшим табло для отображения ставки и выигрыша.

Стоп-символы

Обычные (не прогрессивыне) видео слоты имеют от 35 до 50 стопов на колесо, когда электронные версии слотов могут иметь от 64 до 256, которые проецируются на 22-е ячейки реального(или эмулируемого) колеса.

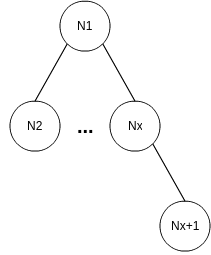
Если бы у вас была возможность заглянуть во внутрь электромеханической слот машины, то вы бы увидели колесо похожее на это(схематическая и развернутая версия):

Символы распределены по 22-м ячейкам. Пустые ячейки - это стопы. Можно предположить, раз существует 11 пустых ячеек, то вероятность того что они выпадут стремится к 50% и т.к. есть только один символ jackpot, то его его вероятность, стало быть, 1 к 22. На самом деле это не так. В действительности машина не оперирует 22-мя ячейками. Она оперирует 128 ячейками(или более) контролируемых программно. Один из символов может быть привязан несколько раз на конкретную стоп позицию барабана. А ГСЧ в свою очередь генерирует значение в пределах 1 до 128. Гипотетическая таблица, кот. демонстрирует как символы привязаны к реальной позиции:

Значения ГСЧ	Символ Барабана	Сколько раз символ встречается на барабане
1-73	Blank	73
74-78	Cherry	5
79-94	Bar	16
95-107	Double Bar	13
108-118	Triple Bar	11
119-126	Red 7	8
127-128	Jackpot	2

Допустим, ГСЧ выдал значение 53 - это пустой символ, после вращения, барабан остановится на соответствующей ячейке. 76 - символ Cherry, 128 - jackpot и т.д.

Распределение организовано так, что чаще выпадают те символы, которые не дают большого выигрыша(средневзвешенное колесо). Некоторые символы будут выпадать чаще остальных, даже если на физическом колесе(или его эмуляторе) оно присутствует в единственном экземпляре. Как можно догадаться, реальный шанс срыва jackpot-а не равняется 1 к 22, и в нашем случае - 2 к 128 или 1 к 64. Большинство символов - это пустые ячейки(73 из 128), что составляет 57%.

Говоря о пустых символах, нужно отметить, когда он выпадает, то это не просто абстрактный символ, а символ с определенным значением(или индексом). Сказанное справедливо и для остальных символов. Мы подходим к вопросу о весе каждой ячейке на барабане. Ниже упрощенная версия таблицы:

Номер стоп-а	Символ	Значение ГСЧ	Вес символа
1	Cherry	1-2	2
2		3-7	5
3	Bar	8-12	5
4		13-17	5
5	Red 7	18-25	8
6		26-30	5
7	Bar	31-35	5
8		36-41	6
9	Cherry	42-43	2
10		44-49	6
11	2 Bar	50-56	7
12		57-62	6
13	Cherry	63	1
14		64-69	6
15	2 Bar	70-75	6
16		76-81	6
17	Bar	82-87	6
18		88-93	6
19	3 Bar	94-104	11
20		105-115	11
21	Jackpot	116-117	2
22		118-128	11

Последняя колонка - это удельный вес символа. Мы имеем 2 из 128 для превого cherry символа и 8 из 128 для семерки. Можно обратить внимание, как jackpot окружен пустыми ячейками с относительно большим удельным весом. Это должно порождать эффект “я был близок к победе”. Т.е. данный символ достаточно часто будет отображаться на экране, но крайне редко выпадать. 

Мы сейчас рассмотрели работу только одного колеса. В жизни количество колес может варьироваться от 3-х до 5-и и каждое из них может иметь свою конфигурацию.

Расчет выигрыша

Зная удельный вес каждого символа, можно построит таблицу окупаемости(payback). Какой процент денег машина возвращает игроку в случае бесконечной игры: 

Комбинация	Выплата	Вероятность	Расчет вероятности	Вероятность x Выплату
3 Jackpot	1666	0.000004	2/128 * 2/128 * 2/128	0.7%
7 7 7	300	0.000244	8/128 * 8/128 * 8/128	7.3%
3 Triple Bar	100	0.000635	11/128 * 11/128 * 11/128	6.4%
3 Double Bar	50	0.001048	13/128 * 13/128 * 13/128	5.2%
3 Single Bar	25	0.001953	16/128 * 16/128 * 16/128	4.9%
3 of any bar	12	0.030518	(16+13+11)/128 * (16+13+11)/128 * (16+13+11)/128	36.6%
3 cherries	12	0.000060	5/128 * 5/128 * 5/128	0.1%
2 cherries	6	0.004399	((5/128)*(5/128)*(128-5)/128)x3	2.6%
1 cherry	3	0.108211	(5/128*(128-5)/128*(128-5)/128)*3	32.5%
				96.3%

Формула расчета для 2 cherries: (вероятность 1-го колеса)*(вероятность 2-го колеса)*(обратную вероятность 3-го колеса), резульат умножаем на 3.  Формула расчета для 1 cherry: (вероятность 1-го колеса)*(обратную вероятность 2-го)*(обратную вероятность 3-го), результат умножается 3. Под фразой обратная вероятность имеется ввиду наступление противоположного события.

96.3% значит, что если я буду играть бесконечно долго, то на каждую ставку в 1$ получал бы обратно лишь 96.3 цента. И чем дольше я играю, тем больше мой проигрыш  стремиться к значению 3.7%.

Ресурсы

• Оригинальная статья
• Словарь терминов на английском
• Словарь терминов на русском
• Немного теории 
• Wizard of Odds

Сказ о том, как перформанс памятью убить

История начинается так… после очередного мержа и запуска проекта, обнаружилось, что производительность приложения упала почти до нуля. Загрузка CPU показывала почти 100%, что в свою очередь приводило к неимоверно долгой обработки запросов. После беглого анализа выяснилось, что тормозит собственно JVM. Как водится в таких случаях, начинаешь листать историю комитов с большей любознательность. В моем случае не было ничего подозрительного, что могло бы приводить к подобной картине. Немного подумав… запустил jvisualvm. Увидел приблизительно следующее:

Первая мысль… есть код, создающий большое количество мелких объектов, которые почти сразу же утилизируются сборщиком мусора. Или тоже самое, но только не в цикле, а во множестве тредов. Еще раз взглянул на историю комитов - ни тени компромата. Немного поразмыслив, обратил внимание на процентное отношение используемой памяти heap-а к доступной. Об этом и поговрим…

Незатейливый код

import java.util.ArrayList;
import java.util.Collection;
public class Main {
    public static void main(String[] args) throws Exception {
        final Collection data = new ArrayList();
        final Runtime runtime = Runtime.getRuntime();
        final int memoryThreshold = Integer.valueOf(args[0]);
        while (true) {

            int memoryUsed = (int) (100 * (runtime.totalMemory() - runtime.freeMemory()) / runtime.totalMemory());
            if (memoryUsed >= memoryThreshold) {
                Thread.sleep(1000);
                continue;
            }

            data.add(new Object());
        }
    }
}

Поясню… Создадим коллекцию и наполним ее объектами, которые не могут быть утилизированы сборщиком мусора. В момент, когда размер используемого heap-а достигнет порогового значения - работаем в холостую, периодически ставя текущий трэд на паузу. В качестве начального порога возьмем 15% от доступной памяти:

java -Xmx5m Main 15

Все чинно, благородно… Следующим шагом увеличим пороговое значение до 80%:

Можно заметить, что значение загрузки CPU подскочило до 70% и GC молотит без остановки. Объяснение я нашел такое… В момент, когда значения израсходованной памяти достигло определенного процента по отношению к доступной, JVM запускает сборщик мусора и, похоже, делает это с высокой степенью упорства и до бескоечности. Проверял на Java 6 и 7 с настройками GC по умолчанию - результат одинаковый.

О том что можно сделать

• В некоторых случаях проблему можно решить увеличением значения Xmx
• Почти уверен, что можно поиграться с опциями GC и получить приемлемые результаты
• Если ни первое, ни второе не помогает, то стало быть остается одно - редизайн той части приложения, которая ест память

Ресурсы

• jvisualvm - сейчас входит в состав JDK
• mat - он же Memory Analyzer