Задача "Скобки"

Не так давно нарвался на интересную задачку в блоге своего знакомого. Дано:

Given a string containing just the characters '(' and ')', find the length of the longest valid (well-formed) parentheses substring. For "(()", the longest valid parentheses substring is "()", which has length = 2. Another example is ")()())", where the longest valid parentheses substring is "()()", which has length = 4.

Или по русски: необходимо найти максимальнодлинную валидную последовательность состаящую из парных скобок. Выражение может быть как вложенным "(())"(с неограниченной глубиной) так и последовательным "()()" с неограниченной длинной, так и состоять из комбинации первых двух. При чем как видно из условия, в выражении могут присутствовать непарные скобки. Так же на просторах можно найти упрощенный вариант - лишь определить валидность выражения, но наша(задача) несколько интересней.

Статья на которую я ссылаюсь дает простое и хорошее решение, но мне захотелось усложнить условия - не использовать стэк. Юнит тест:

@Test
public void testFind() {
    assertEquals(Reference.find("("), Solution.find("("));
    assertEquals(Reference.find(")"), Solution.find(")"));
    assertEquals(Reference.find(")("), Solution.find(")("));
    assertEquals(Reference.find("()"), Solution.find("()"));
    assertEquals(Reference.find("()()"), Solution.find("()()"));
    assertEquals(Reference.find("(()"), Solution.find("(()"));
    assertEquals(Reference.find("(())"), Solution.find("(())"));
    assertEquals(Reference.find("())(()()"), Solution.find("())(()()"));
    assertEquals(Reference.find("(((()())))"), Solution.find("(((()())))"));
    assertEquals(Reference.find("(((((()()))))"), Solution.find("(((((()()))))"));
    assertEquals(Reference.find("()(())"), Solution.find("()(())"));
    assertEquals(Reference.find(")()())"), Solution.find(")()())"));
    assertEquals(Reference.find("()(()"), Solution.find("()(()"));
}

Где:

• Reference.find(String string) - эталонная реализация
• Solution.find(String string) - решение

Первое

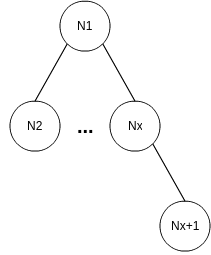
Поигравшись с неправильными решениями(а их было около трех), пришел к следующей модели. Легко заметить, что выражение можно представить в виде перевернутого дерева, где узел - это одна валидная группа состоящая из открывающей и закрывающей скобки плюс вложенные(дочерне ноды). Минимальновалидная нода - это выражение вида "()".

Рессмотрим строку:

(())(()

Тогда первая валидная группа будет иметь следующий вид:

А все выражение целиком состоять из трех подгурпп:

• "(())" - валидная(закрытая или парная) группа длинной 4
• "(" - невалидня группа длинной 1
• "()" - валидная группа длинной 2

Конечное решение выглядит так - обходим строку, пытаясь найти валидную группу начиная с нулевого элемента. Есть два возможных случая:

• Группа парная - производим смещение на позицию вправо равную длинне группы. Если группы идут одна за одной без разрыва, то накапливаем дилнну в нек. переменную-счетчик, если происходит разрыв, то сравниваем накопленное значение с максимальным
• Группа непарная - пропускаем данный элемент и повторяем операцию поиска группы

public class Solution {

    static final class Node {
        int offset;
        int len;
        List<Node> nodes;

        Node(int offset, int len, List<Node> nodes) {
            this.offset = offset;
            this.len = len;
            this.nodes = nodes;
        }

        Node(int offset, int len) {
            this(offset, len, null);
        }

        @Override
        public String toString() {
            return "[offset=" + offset + ", len=" + len + ", child=" + nodes + "]";
        }
    }

    static int find(String string) {
        int max = 0;
        int accumulator = 0;

        for (int i = 0; i < string.length(); i++) {
            Node node = getNode(string, i);
            if (node == null) {
                max = Math.max(max, accumulator);
                accumulator = 0;
                continue;
            }

            accumulator += node.len;
            i += (node.len - 1);
        }

        return Math.max(max, accumulator);
    }


    static Node getNode(final String string, final int offset) {
        if (offset >= string.length()) return null;

        List<Node> nodes = new ArrayList<Node>(0);
        int nodesLen = 0;

        if (string.charAt(offset) == '(') {
            int rightIndex = offset + 1;
            if (rightIndex >= string.length()) return null;

            boolean right = string.charAt(rightIndex) == ')';
            if (right) return new Node(offset, 2);

            for (int i = (offset + 1); i < string.length(); i++) {
                Node node = getNode(string, i);

                if (node != null) {
                    nodes.add(node);
                    i += (node.len - 1);
                    nodesLen += node.len;
                }
            }
            if (nodes.isEmpty()) return null;

            rightIndex = offset + nodesLen + 1;
            if (rightIndex >= string.length()) return null;

            right = string.charAt(rightIndex) == ')';
            if (right) return new Node(offset, 2 + nodesLen, nodes);
        }

        return null;
    }
}

Как можно заметить есть ряд существенных недостатков, а именно:

• Рекурсия - при большой глубине вложенности скобок, запустив тест, гарантированно получим переполнение стэка
• Громоздкость - что не говори, а строить дерево относительно ресурсоемкая операция по сравнению с оригинальным решением
• Время работы(пересекается с предыдущим) - далеко не самое лучшее

Чуть позже я немного упростил код - убрал класс Node, оставив лишь только длинну группы(метод getNode - возвращет не экземпляр класса, а значение типа integer). Но приводить код смысла нет, т.к. в основе лежит все та же убогая идея.

Второе

Позже сфорировал ряд дополнительных требований к реализации - она должно быть итеративной и не такой ресуроемкой. За основу взял следующую идею - объявляем переменные:

• left - счетчик окрывающих скобок. Делаем инкремент каждый раз когда всречается окрывающая скобка.
• right - счетчик закрывающих скобок. Делаем инкремент каждый раз когда всречается закрывающая скобка.
• pair - счетчик валидных пар. Делаем инкремент каждый раз когда счетчик left и right больше нуля.

Последоватлеьно обхоим всю строку, так же как и в предыдущем варианте пытаемся найти валидную(закрытую) группу, но делаем это не рекурсивно, а итеративно. Встречая валидную группу, смещаемся в право по строке на ее длинну. В случае невалидной группы - смещаемя вправо на один символ. Строка разбитая на группы будет выглядеть следующим образом:

А решение целиком:

public class Solution {


    static int find(String string) {
        int max = 0, len = 0;
        for (int i = 0; i < string.length(); i++) {
            int n = find(string, i);
            if (n > 0) {
                len += n;
                i += (n - 1);
            } else {
                max = Math.max(len, max);
                len = 0;
            }
        }
        return Math.max(len, max);
    }

    static int find(String string, int index) {
        int left = 0, right = 0, pair = 0;
        for (int i = index; i < string.length(); i++) {

            if (string.charAt(i) == '(') {
                left++;
            } else {
                if (left <= 0) continue;
                right++;
            }

            if (left > 0 && right > 0) {
                left--;
                right--;
                pair++;
            }

            if (left == 0 && right == 0) break;
        }
        return (left == 0 && right == 0) ? pair * 2 : 0;
    }
}

Ресурсы

• Оригинальная статья
• Упрощенная вариация задачи
• Проект на bitbucket-е(по хронологии): раз, два, три